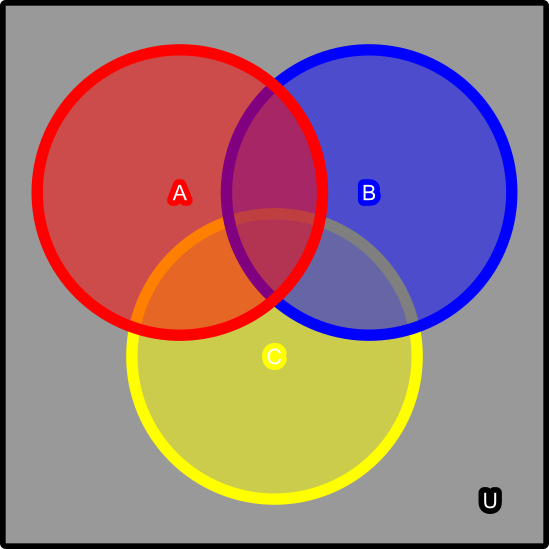
Outlining the Question
Let ![]() ,
, ![]() , and
, and ![]() be sets with dependent probabilities.
be sets with dependent probabilities.
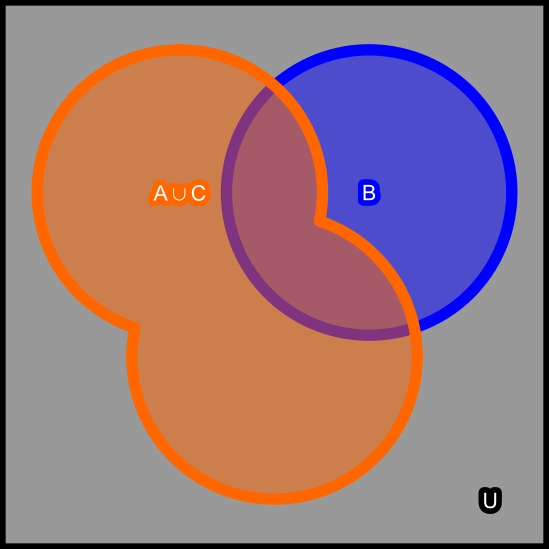
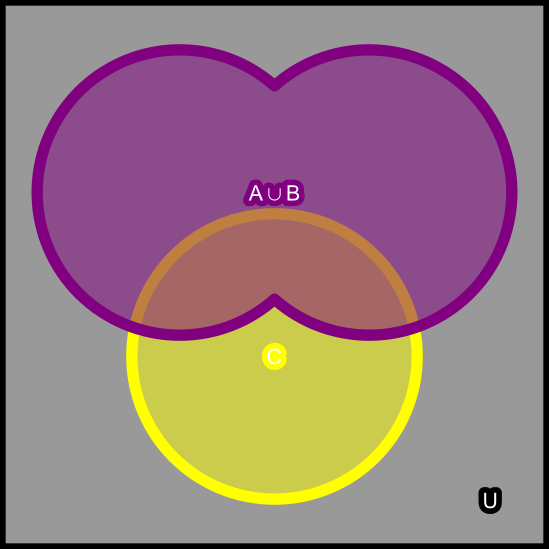
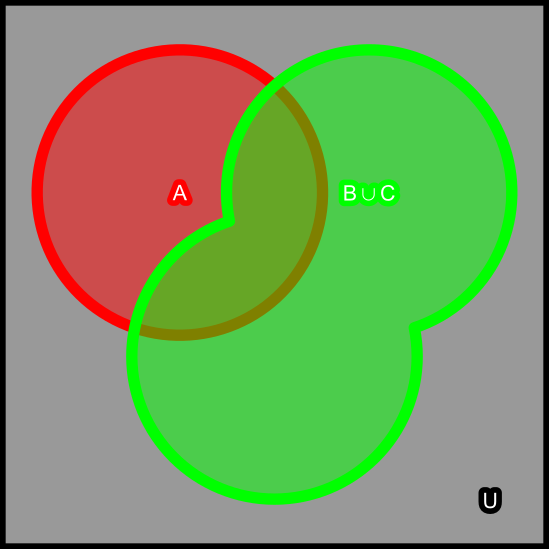
Suppose:
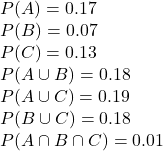
1a. Find
![]()
Response
![]()
I need to calculate it
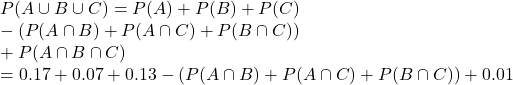
I am still struggling to find the intersections of all of these. But I figured I could calculate the unions.
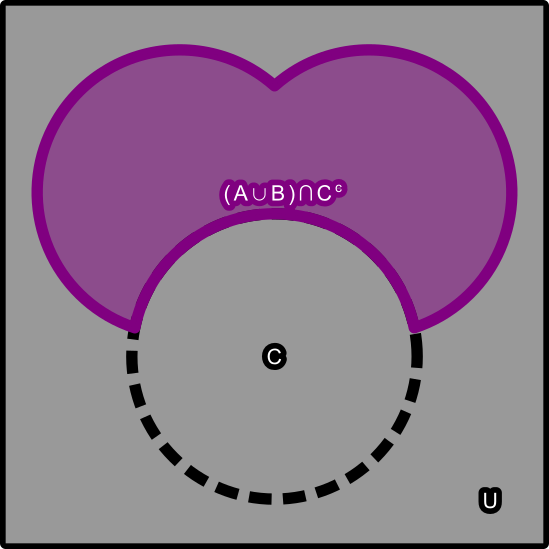
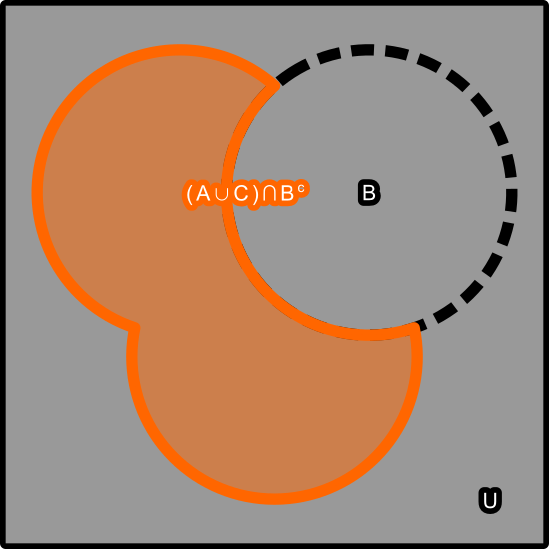
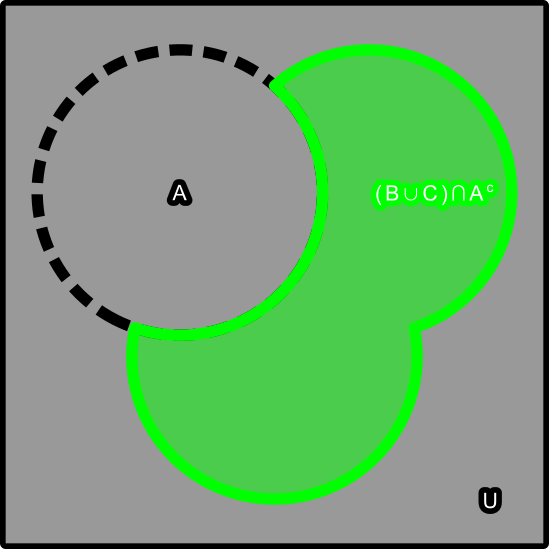
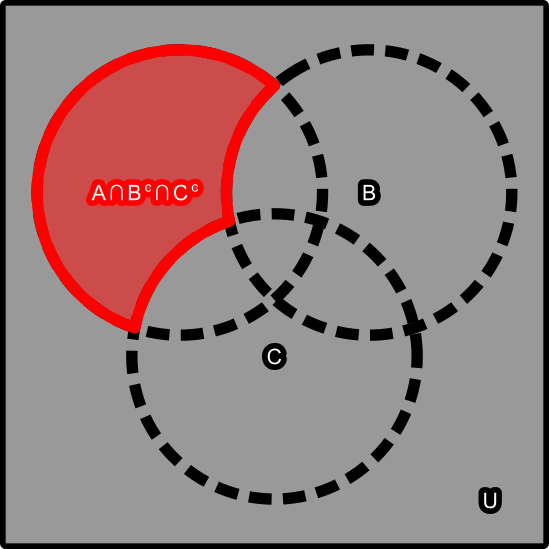
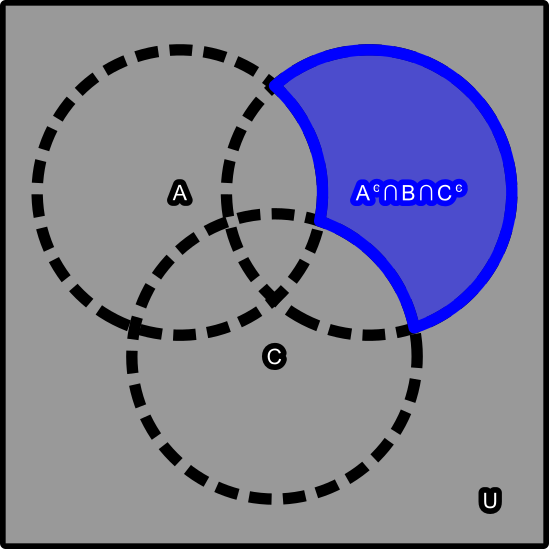
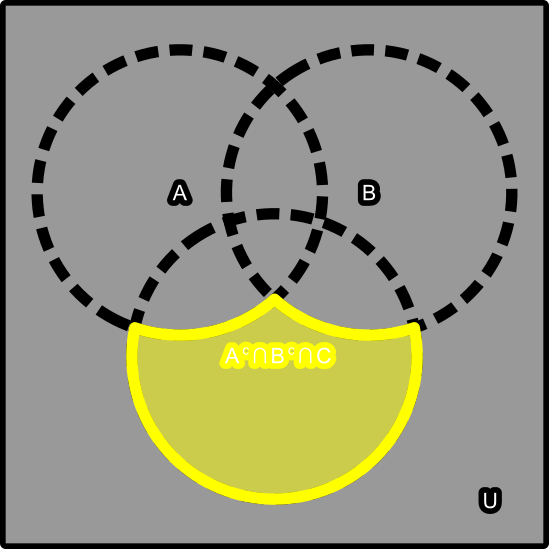
But how to isolate for any of these?
Eureka!
While tinkering I realized that the two probabilities can be extracted:
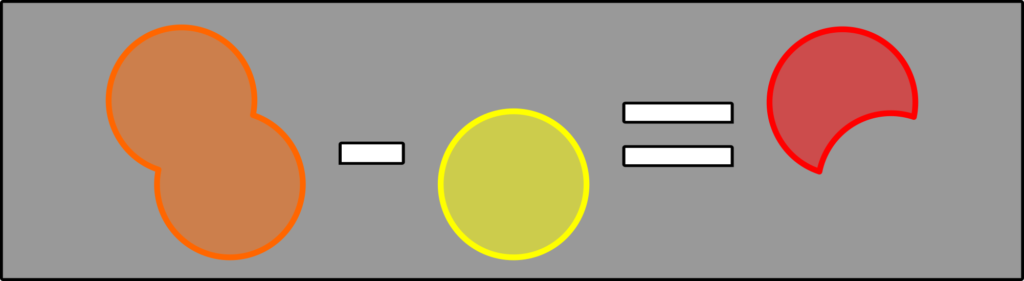
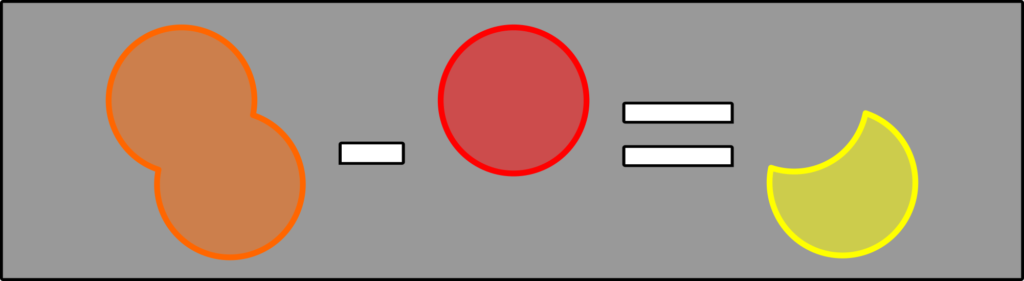
If you add up the individual probabilities and subtract the union, you end up with the intersection! Visually it looks like this:
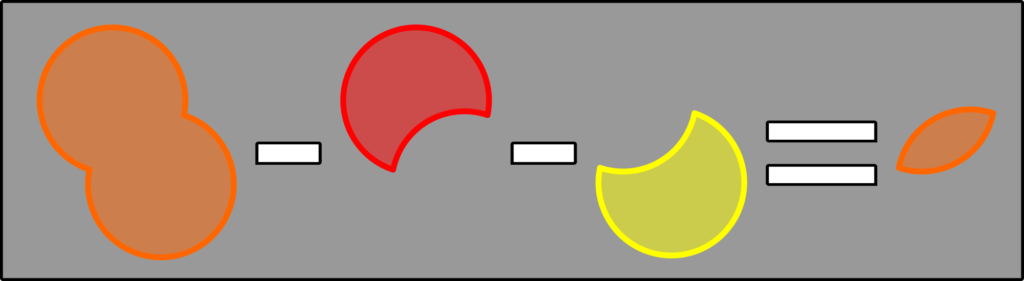
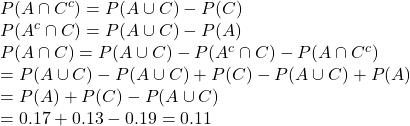
Updating the visual to match the simplified equation:
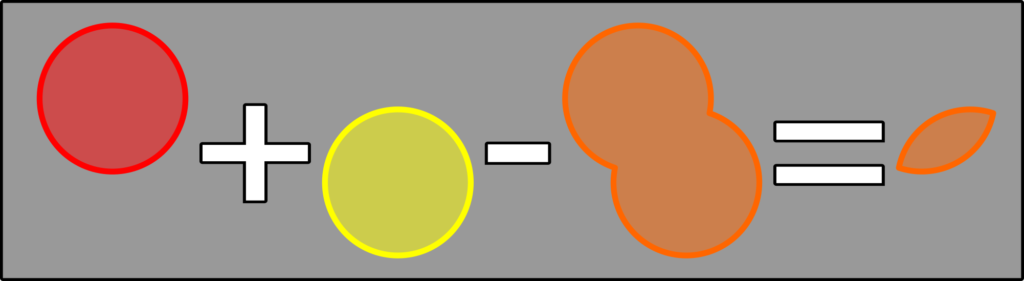
And now that I see it, of course it makes sense!
We can do the same for the others:
![]()
And:
![]()
So then:
![]()
And finally:
![]()
1b. Find
![]()
Response
Now that we have isolated the intersections.
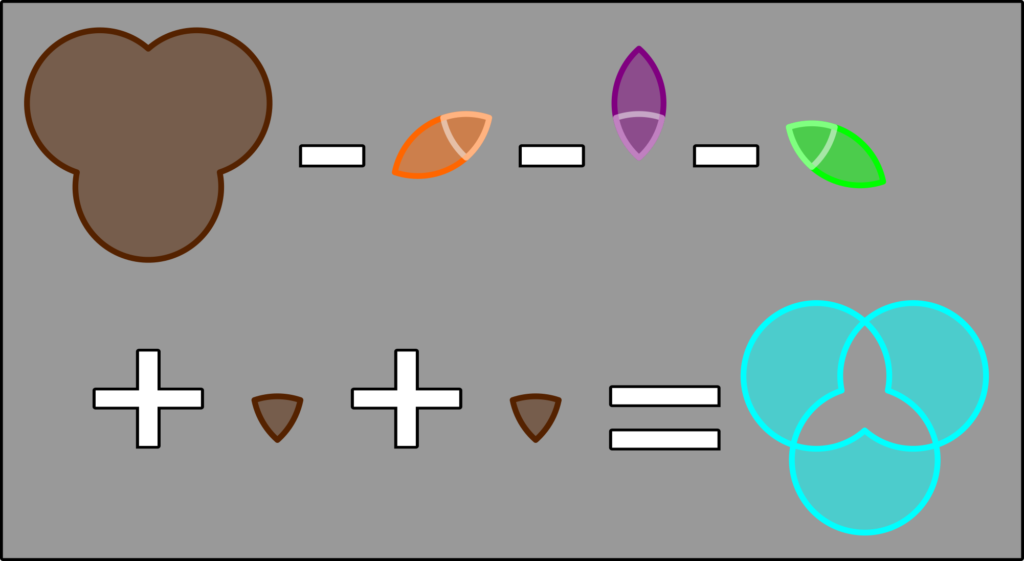
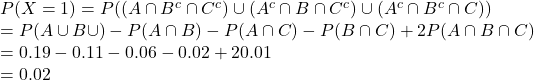
1c. Find
![]()
Response
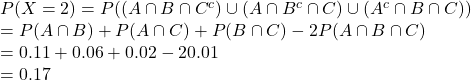
1d. Find
![]()
Response
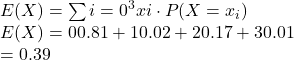
1e. Find
![]()
Response
![]()
LoTUS states that:
![]()
1f. Find
![]()